SISTEMA OCTAL

                           SISTEMA OCTAL

 

El sistema numérico en base 8 se llama octal y utiliza los dígitos del 0 al 7. En informática a veces se utiliza la numeración octal en vez de la hexadecimal. Tiene la ventaja de que no requiere utilizar otros símbolos diferentes de los dígitos. Sin embargo, para trabajar con bytes o conjuntos de ellos, asumiendo que un byte es una palabra de 8 bits, suele ser más cómodo el sistema hexadecimal, por cuanto todo byte así definido es completamente representable por dos dígitos hexadecimales.

Tabla de conversión entre decimal, binario, hexadecimal y octal

Decimal	Binario	Hexadecimal	octal
0	00000	0	0
1	00001	1	1
2	00010	2	2
3	00011	3	3
4	00100	4	4
5	00101	5	5
6	00110	6	6
7	00111	7	7
8	01000	8	10
9	01001	9	11
10	01010	A	12
11	01011	B	13
12	01100	C	14
13	01101	D	15
14	01110	E	16
15	01111	F	17

Cambio de base

De base decimal a base octal

Veamos el método para pasar del sistema decimal al sistema octal mediante un ejemplo. Escribiremos el número 768 (base 10) en base octal (base 8):

1. Dividimos el número entre 8:

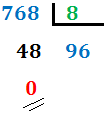
2. Si el cociente es mayor o igual que 8, lo dividimos entre 8. En nuestro caso, el cociente es 96 (mayor que 8), por lo que lo dividimos de nuevo: 

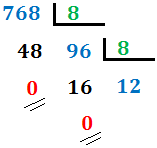
3. Continuamos así hasta obtener un cociente menor que 8. En nuestro caso, el cociente es 12 (mayor que 8), así que lo dividimos de nuevo:

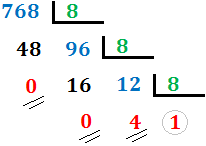
El cociente es 1, menor que 8, con lo que hemos terminado el proceso. Hemos indicado los restos con dos rayas y el último cociente con una circunferencia.

4. El número en base 8 es: (Último cociente) (Último resto) (Penúltimo resto)... (Segundo resto) (Primer resto). En nuestro caso, el último cociente es 1, el último resto es 4, el penúltimo resto es 0 y el primer resto es 0. Por tanto, el número 768 en base octal es 1400.